Research Projects - BITS Pilani

Research

Research Interests

Statistical Mechanics.
Disordered Systems.
Phase Transition and Critical Phenomena.
Linear Elastic Fracture Mechanics (LEFM).
Seismic events & Earthquake Statistics.
Porous Media.
Effective Rheology of Multi-phase Flow.
Propagating Interface Through Disordered Systems - Mechanical and Fluid.
Quantum Dot Synthesis and Evolution.

Gist of Research

My main research interest is studying statistical mechanical systems in presence of disorder and acted by an external perturbation. Understanding the time evaluation of such disordered systems is fascinating owing to to their rich dynamics, including highly nonlinear, out-of-equilibrium behavior, self-organization and enchanting patterns. Statistical physical models of such systems yields constitutive laws that do not only explain the behavior but also prove highly useful in various applications. Understanding the origin and dynamics of such a disorder systems provides insight into phenomena such as failure of solids, multi-phase flow, snow avalanches, seismic events, and more, making such studies important from the point of view of various branches of engineering, material science, and geophysics.

Expertise

I developed expertise in a wide range of statistical mechanics approaches and tools like models for critical behavior, phase transition, self-organized criticality, and multi-fractal nature of local parameters, for both solid mechanics (deformation and failure) and fluid mechanics of multi-phase flow in porous media. I also gained expertise in numerical tools: I developed simulators for avalanche dynamics during a failure process as well as interface propagation for multi-phase flow using C and C++ language, and performed data analysis on acoustic emission experiments and earthquake statistics using Python and Jupyter notebook as well as Matlab and Mathematica.

Overview

Statistical Modeling of Fracture

It is been over three decades now that statistical physicists started paying continual attention to the failure and breakdown properties of disordered materials. Primarily its importance lies in the extreme nature of the statistics, translating into safety and integrity issues for large as well as small structures. It also has the fascinating aspect of universality in its response statistics that opened up new applications of concepts of phase transition and criticality in this field [Phil. Trans. Royal Society A, vol 377, Issue 2136 (2018)]. One of the interesting questions in this regard is the forewarning of breakdown [Sci. Rep. vol 5, no 13259 (2015)]. Other than the nature of the acoustic signals [Phys. Rev. Lett. 73, 3423 (1994)] (Fig.1) emitted prior to a breakdown, even simply the duration of such signals is crucially important. It is well known that a higher disordered sample has more prior warnings of its imminent breakdown. A brittle material (like glass), on the other hand, will have an understandably shorter time window for such signals. The system size scaling, and the probability distribution functions of the failure times of disorder materials have been actively pursued questions.

During my Ph.D. (with Prof. Purusattam Ray) I have extensively explored statistical disordered systems, focusing on their rheological response under external stress and predict the nature of failure (brittle vs ductile), to eventually provide a warning of catastrophic events. Using methods such as Monte Carlo and Molecular Dynamics simulations, I was able to explain the mode of failure [Europhysics Letters, Volume 112, Number 2, pp 26004 (2015), Phys. Rev. E 96, 042142 (2017)] and spatial correlation of damage during crack propagation in a discrete or continuum media [Phys. Rev. E 91, 050105(R) (2015), Front. Phys. 9, 752086 (2021), Phys. Rev. E 105, 055003 (2022)]. We exposed the existence of two main parameters, (i) strength of disorder and (ii) stress release range, that control the dynamics and determine if the failure process is brittle or ductile as well as if it is nucleating or percolating [Phys. Rev. E 96, 063003 (2017), Physica A 569, 125782 (2021)] (Fig.2). Above two parameters has a significant role as the formal depends on material property like crystal defects, impurities, micro-crack, etc., while the latter is related to the span of fracture process zone and the stress concentration. These papers provided a through understanding of fracturing and failure at the microscopic scales.

During my Postdoctoral research in the University of Tokyo (With Prof. T. Hatano) I moved to study fracturing on larger scales relevant to geo-hazards such as seismic events and snow avalanches. We developed a framework to quantitatively predict the dynamics of fracture propagation, providing insights to creep failure [Phys. Rev. Res. 4, 023110 (2022), Phys. Rev. Research 2, 023104 (2020)]. Our theory was shown to favourably compare with data of the acceleration and deceleration measured before and after earthquakes (the main shock, characterized by inverse Omori and Omori-Utsu law) [Phys. Rev. E 97, 062149 (2018)] (Fig.3), which is invaluable for earthquake prediction and warning.

Effective Rheology of Multi-phase Flow

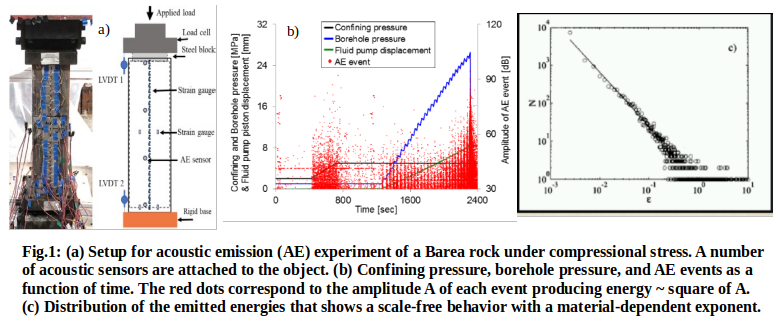
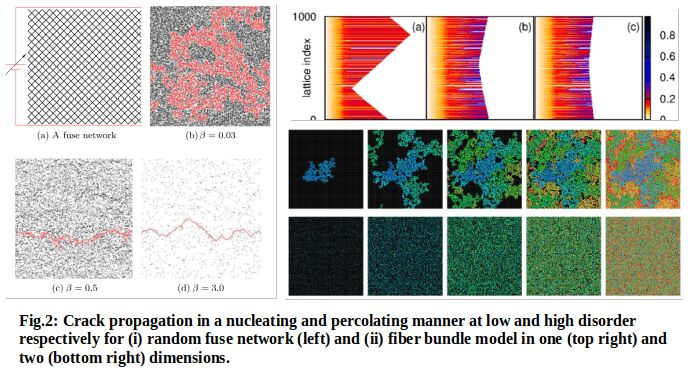
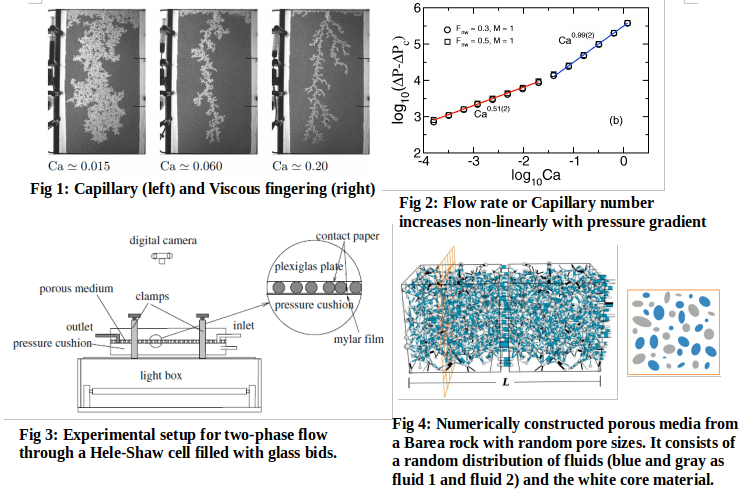
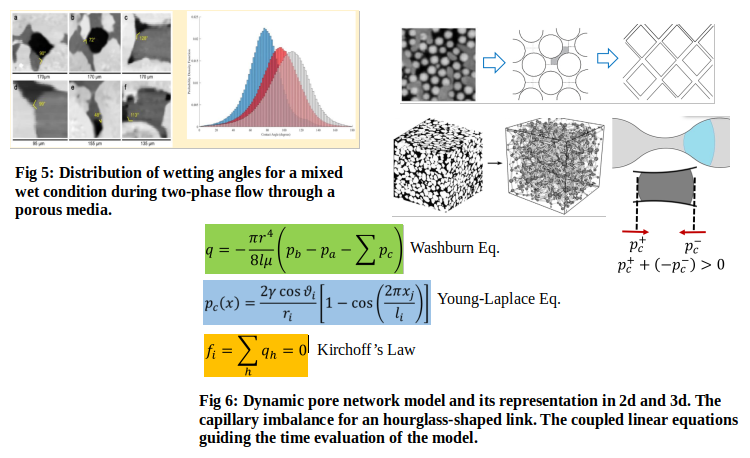
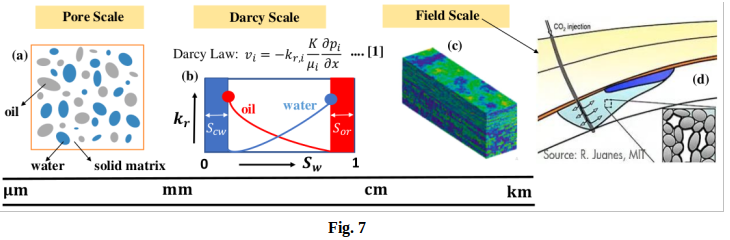
The study of multi-phase flow, on the other hand, involves understanding the behavior of large scale processes (oil recovery, CO2 sequestration, groundwater collection, blood flow in capillary vessels, etc.) by breaking down the dynamics of fluid in the pore-scale [J. Bear, Dynamics of Fluids in Porous Media]. In the pore scale, when two immiscible fluids ow in a porous media the flow does not obey linear Darcy law [Transp. Porous Med. 1, 3 (1986)] in the regime where the capillary forces are comparable to the viscous forces. The transient behavior of the model shows viscous fingering, capillary fingering, and stable displacement depending on driving parameters such as capillary number or the viscosity ratio (Fig.1). In the steady-state, the flow rate was observed both numerically [Europhys. Lett. 99, 44004 (2012)] and experimentally [Phys. Rev. Lett. 102, 074502 (2009)] to scale in a quadratic manner with the pressure gradient (Fig.2). The disorder in capillary barriers at pores effectively creates a yield threshold in the porous medium, introducing an overall threshold pressure in the system making the fluids reminiscent of a Bingham viscoplastic fluid [Europhys. Lett. 4(1), 1227 (1987)].

My second postdoctoral position (with Prof. Alex Hansen) at Porous Media Laboratory (Porelab), the world’s leading institution for physics of porous media, provided me with the opportunity to expand my research horizons into the fascinating field of rheology of complex fluids flowing in a porous material. I developed a theoretical framework that was able to reproduce controlled experiments (using the highly useful Hele-Shaw cell (Fig.3), similar to those proposed in this fellowship, as model system). An experimental validation is very important in our case since many of the theories that we proposed is novel in the context of porous media. We explained the non-linear rheology in the intriguing (and practically important) case where both capillary and viscous forces are comparable. Of particular interest is how the structure of a porous material and its wetting properties influence the rheology. We were able to provide an extensive systematic quantification of the role of pore-scale heterogeneity in pore sizes [Front. Water 3, 709833 (2021)] (Fig.4), wetting angles [Transport in Porous Media 139, 491 (2021)] (Fig.5), and fluid distribution [Front. Phys. 7, 92 (2019)] (Fig.4). In Porelab I gained experience in the state of the art techniques, both computational and experimental.

I gained expertise in computational fluid dynamics, to develop a discrete, pore scale dynamic pore network modelling (DPNM) [Front. Phys. 8, 548497 (2021)] (Fig.6). DPNM provides a mechanistic efficient methodology, as it relies on basic physical rules resolved for an idealised geometrical description of links and nodes. DPNM solves three coupled linear equations: Washburn equation (for potential flow), Young-Laplace equation (capillary pressure), and Kirchhoff’s law (mass balance), through a conjugate gradient solver. Experimentally, we used Hele-Shaw cells (Fig.3), idealised model systems in which all properties are known and controlled but still exhibit the essential features of potential flow in confined porous media.

We used the combination of computational and experimental techniques to develop a novel thermodynamic framework for flow through porous media [Front. Phys. 8, 4 (2020)] which is consistent with theoretical and experimental data of relative permeability [Transport in Porous Media 143, 69 (2022)], the main characteristic of flow in porous media used in the industry. This framework is highly relevant and thus highly useful for the upscaling process (Fig.7) that links pore-scale, Darcy scale and field scale to each other.

Experimental Laboratory for Multi-Phase Flow

Coming Soon

Integrated first degree

Higher Degree

Doctoral Programmes

Student Services

Student Activities

Integrated First Degree

Higher Degree

Doctoral Programmes

WILP

Dubai Campus

Give us your feedback

Upload Screenshot

Dr. Subhadeep Roy